Strain measurement and analysis

Understanding strain and its effects

When materials experience forces, their internal atomic arrangements deform. This deformation, called strain (\(\varepsilon\)), reveals crucial information about a material’s structure and behavior. Consider bending a metal beam: some parts stretch (\(\varepsilon > 0\)), others compress (\(\varepsilon < 0\)), creating a complex pattern of internal deformation. At the atomic scale, these deformations appear as subtle changes in the spacing (\(d\)) and arrangement of atoms within the crystal lattice.

What is the main principle behind 4D-STEM strain measurement?

\[\varepsilon = \frac{d_{\text{strained}} - d_{\text{ref}}}{d_{\text{ref}}} = \frac{g_{\text{ref}} - g_{\text{meas}}}{g_{\text{meas}}} = \frac{\partial u}{\partial x}\]

Mathematical framework

To describe these deformations precisely, we use the strain tensor \(\boldsymbol{\varepsilon}\):

\[\begin{split}\boldsymbol{\varepsilon} = \begin{bmatrix} \varepsilon_{xx} & \varepsilon_{xy} \\ \varepsilon_{yx} & \varepsilon_{yy} \end{bmatrix}\end{split}\]

Each element of this tensor represents a distinct type of deformation. Below is a visualization illustrating how each strain component affects a grid of points, simulating the atomic lattice:

(Source code, png, hires.png, pdf)

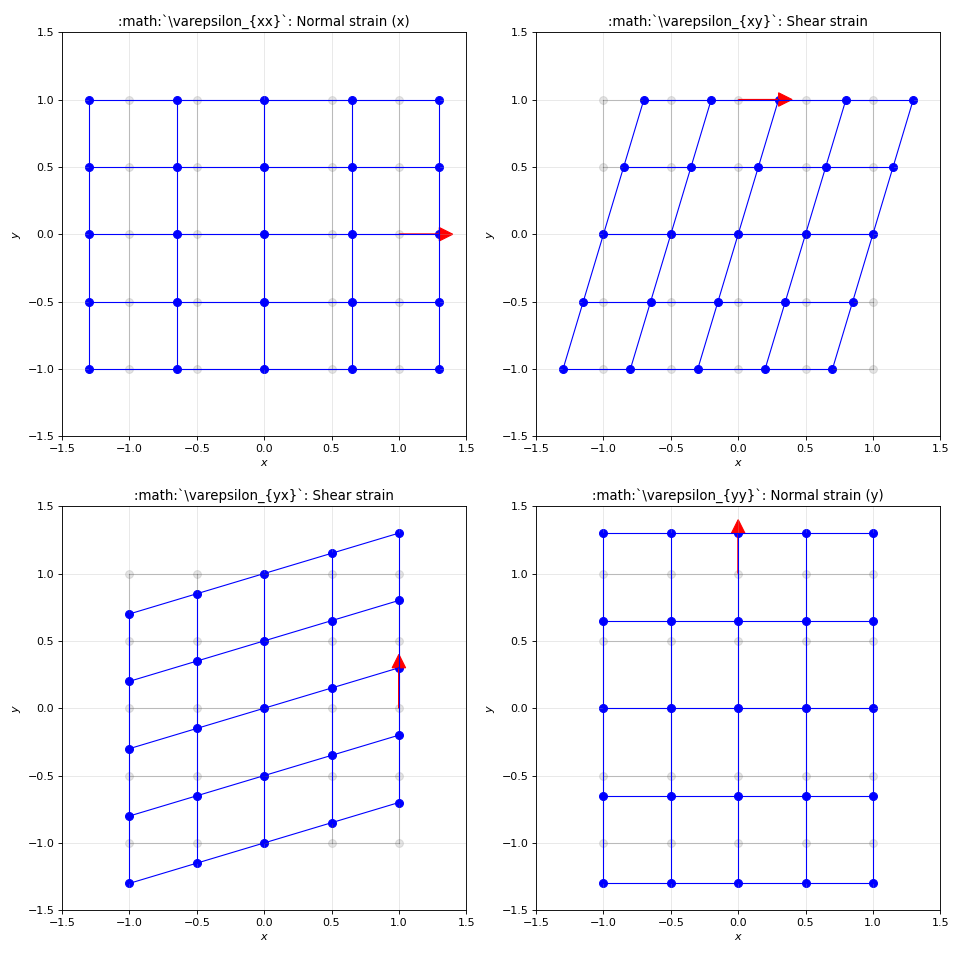
How do you then find the strain tensor from these spot shifts?

We can derive this through several key steps:

First, let’s define the displacement gradient tensor \(\mathbf{D}\). When a crystal deforms, each point moves by a displacement vector \(\mathbf{u}(\mathbf{r})\). The displacement gradient tensor describes how this displacement changes with position:

\[\begin{split}\mathbf{D} = \begin{pmatrix} D_{xx} & D_{xy} \\ D_{yx} & D_{yy} \end{pmatrix} = \begin{pmatrix} \frac{\partial u_x}{\partial x} & \frac{\partial u_x}{\partial y} \\ \frac{\partial u_y}{\partial x} & \frac{\partial u_y}{\partial y} \end{pmatrix}\end{split}\]

where \(u_x\) and \(u_y\) are the displacement components in the x and y directions.

The displacement gradient tensor \(\mathbf{D}\) contains both deformation (strain) and rotation:

\[\mathbf{D} = \underbrace{\frac{1}{2}(\mathbf{D} + \mathbf{D}^T)}_{\text{strain }\boldsymbol{\varepsilon}} + \underbrace{\frac{1}{2}(\mathbf{D} - \mathbf{D}^T)}_{\text{rotation }\boldsymbol{\omega}}\]

The symmetric part \(\boldsymbol{\varepsilon}\) represents true strain (changes in lengths and angles), while the antisymmetric part \(\boldsymbol{\omega}\) represents rigid-body rotation. In strain analysis, we’re usually interested in the strain part \(\boldsymbol{\varepsilon}\), since rotation doesn’t cause internal deformation.

How can general deformation can be decomposed into pure strain and rotation?

(Source code, png, hires.png, pdf)

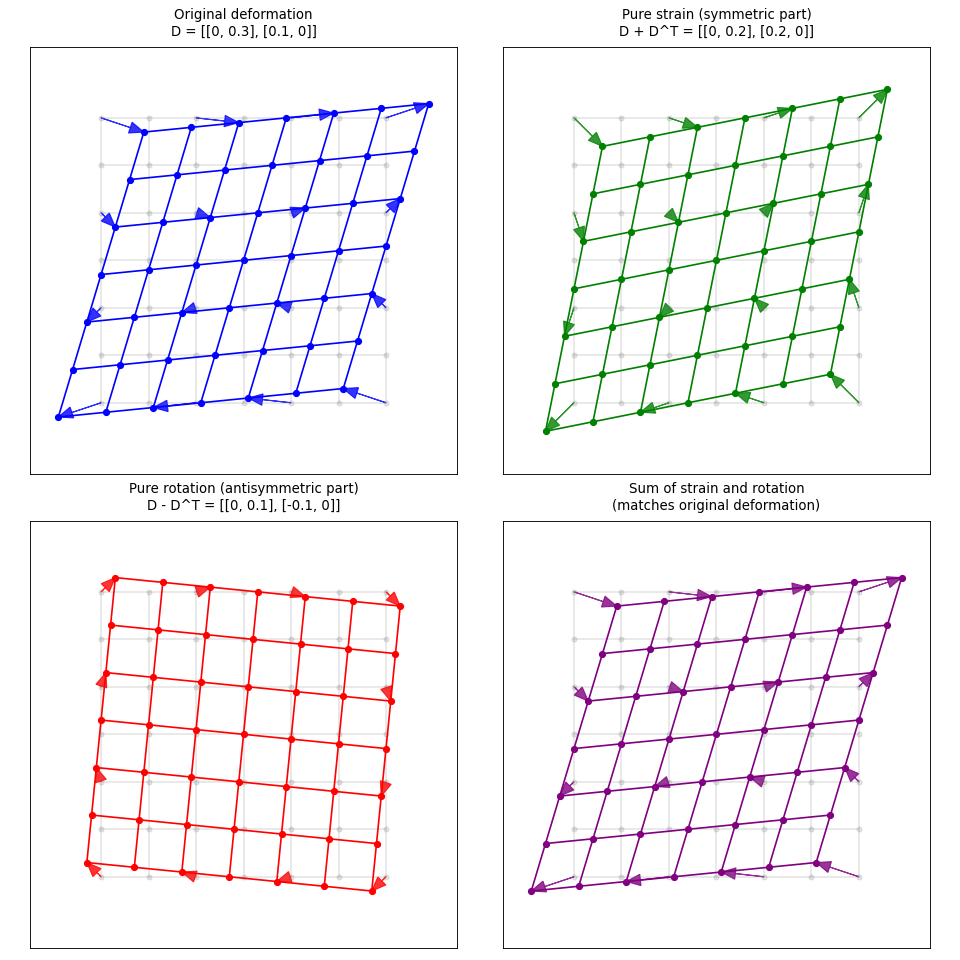
Decomposition of displacement gradient tensor into pure strain (changes in lengths/angles) and pure rotation.

Why do we use \(\frac{1}{2}(\mathbf{D} + \mathbf{D}^T)\) for strain and \(\frac{1}{2}(\mathbf{D} - \mathbf{D}^T)\) for rotation?

Think about what strain and rotation mean physically:

1. Strain (stretching/compression):

   • Should be the same whether you measure from left-to-right or right-to-left

   • Should be the same whether you measure from top-to-bottom or bottom-to-top

   • This means: swapping any two points should give the same deformation

   • Mathematically: \(D_{xy} = D_{yx}\) (symmetry)

2. Rotation:

   • Moving from left-to-right should be opposite to moving from right-to-left

   • Moving from top-to-bottom should be opposite to moving from bottom-to-top

   • This means: swapping two points should reverse the movement

   • Mathematically: \(D_{xy} = -D_{yx}\) (antisymmetry)

Let’s see why \(\frac{1}{2}(\mathbf{D} + \mathbf{D}^T)\) gives us strain. For any matrix:

\[\begin{split}\mathbf{D} = \begin{pmatrix} D_{xx} & D_{xy} \\ D_{yx} & D_{yy} \end{pmatrix}\end{split}\]

The symmetric part \(\boldsymbol{\varepsilon}\) is:

\[\begin{split} \boldsymbol{\varepsilon} = \frac{1}{2}(\mathbf{D} + \mathbf{D}^T) = \frac{1}{2}\begin{pmatrix} 2D_{xx} & D_{xy} + D_{yx} \\ D_{xy} + D_{yx} & 2D_{yy} \end{pmatrix}\end{split}\]

The antisymmetric part \(\boldsymbol{\omega}\) is:

\[\begin{split}\boldsymbol{\omega} = \frac{1}{2}(\mathbf{D} - \mathbf{D}^T) = \frac{1}{2}\begin{pmatrix} 0 & D_{xy} - D_{yx} \\ D_{yx} - D_{xy} & 0 \end{pmatrix}\end{split}\]

Now, look what happens when we add D and D^T:

In strain (symmetric) parts:

• Points moving left-to-right: \(D_{xy}\)

• Points moving right-to-left: \(D_{yx}\)

• When we add and divide by 2: \(\frac{D_{xy} + D_{yx}}{2}\)

• This averages the deformation in both directions → pure strain!

In rotation (antisymmetric) parts:

• Points rotating clockwise: \(D_{xy}\)

• Points rotating counterclockwise: \(-D_{yx}\)

• When we subtract and divide by 2: \(\frac{D_{xy} - D_{yx}}{2}\)

• This captures the difference in directions → pure rotation!

The factor of \(\frac{1}{2}\) appears because we’re averaging the effects in both directions.

Simple example: If a point moves: - Right by 2 units (\(D_{xy} = 2\)) - Up by 1 unit (\(D_{yx} = 1\))

Then: - Strain = \(\frac{2 + 1}{2} = 1.5\) (average deformation) - Rotation = \(\frac{2 - 1}{2} = 0.5\) (difference indicating rotation)

The total movement (D) is perfectly split into these two components!

How do diffraction spot shifts relate to strain?

1. Real space deformation This displacement gradient tensor \(\mathbf{D}\) relates deformed lattice vectors to reference vectors:

   \[\mathbf{a}_i = (\mathbf{I} + \mathbf{D})\mathbf{a}_i^{\text{ref}}\]

   where \(\mathbf{I}\) is the identity matrix.

2. Reciprocal lattice relationship The real and reciprocal lattice vectors are connected by:

   \[\mathbf{g}_i \cdot \mathbf{a}_j = 2\pi\delta_{ij}\]

3. Apply deformation Substituting the deformed lattice vectors:

   \[\mathbf{g}_i \cdot (\mathbf{I} + \mathbf{D})\mathbf{a}_j = 2\pi\delta_{ij}\]

   In the reference state:

   \[\mathbf{g}_i^{\text{ref}} \cdot \mathbf{a}_j^{\text{ref}} = 2\pi\delta_{ij}\]

   Therefore:

   \[\mathbf{g}_i \cdot (\mathbf{I} + \mathbf{D}) = \mathbf{g}_i^{\text{ref}}\]

4. Solve for reciprocal vectors Multiply both sides by \((\mathbf{I} + \mathbf{D})^{-1}\):

   \[\mathbf{g}_i = \mathbf{g}_i^{\text{ref}}(\mathbf{I} + \mathbf{D})^{-1}\]

5. Linearize for small strains For the small deformations typical in 4D-STEM:

   \[(\mathbf{I} + \mathbf{D})^{-1} \approx (\mathbf{I} - \mathbf{D})\]

   Thus:

   \[\boxed{\mathbf{g}_i = (\mathbf{I} - \mathbf{D}^T)\mathbf{g}_i^{\text{ref}}}\]

Why is inverse approximation \((\mathbf{I} + \mathbf{D})^{-1} \approx (\mathbf{I} - \mathbf{D})\) true for small strains?

Think about a simple scalar example first. For any \(|x| < 1\):

\[\frac{1}{1+x} = 1 - x + x^2 - x^3 + ...\]

This is because (1+x)(1-x+x²-x³+…) = 1. The same idea works for matrices:

\[(\mathbf{I} + \mathbf{D})^{-1} = \mathbf{I} - \mathbf{D} + \mathbf{D}^2 - \mathbf{D}^3 + ...\]

In 4D-STEM, strain is typically tiny (0.1-1%), so if we plug in a number:

For 1% strain (\(\|\mathbf{D}\| \approx 0.01\)):

• First order: \(\|\mathbf{D}\| \approx 10^{-2}\)

• Second order: \(\|\mathbf{D}^2\| \approx 10^{-4}\) (100× smaller)

• Third order: \(\|\mathbf{D}^3\| \approx 10^{-6}\) (10000× smaller)

Given these rapidly decreasing magnitudes, we can confidently approximate:

\[(\mathbf{I} + \mathbf{D})^{-1} \approx \mathbf{I} - \mathbf{D}\]

The error from this approximation is on the order of \(\|\mathbf{D}^2\| \approx 10^{-4}\), which is negligible for strain analysis.

What’s the step-by-step process in 4D-STEM strain measurement?

1. Collect reference pattern

   Choose an unstrained region and identify two strong diffraction spots that correspond to reciprocal lattice vectors:

   \[\begin{split}\mathbf{g}_1^{\text{ref}} &= \begin{pmatrix} 2.0 \\ 0.0 \end{pmatrix} \text{ nm}^{-1} \\ \mathbf{g}_2^{\text{ref}} &= \begin{pmatrix} 0.0 \\ 2.0 \end{pmatrix} \text{ nm}^{-1}\end{split}\]

2. Measure strained spots

   For each scan position, record the diffraction spot positions in the strained state:

   \[\begin{split}\mathbf{g}_1^{\text{meas}} &= \begin{pmatrix} 1.98 \\ 0.02 \end{pmatrix} \text{ nm}^{-1} \\ \mathbf{g}_2^{\text{meas}} &= \begin{pmatrix} -0.02 \\ 2.02 \end{pmatrix} \text{ nm}^{-1}\end{split}\]

3. Calculate spot displacements

   Find the difference between measured and reference positions (\(\Delta\mathbf{g} = \mathbf{g}^{\text{meas}} - \mathbf{g}^{\text{ref}}\)):

   \[\begin{split}\Delta\mathbf{g}_1 &= \begin{pmatrix} -0.02 \\ 0.02 \end{pmatrix} \text{ nm}^{-1} \\ \Delta\mathbf{g}_2 &= \begin{pmatrix} -0.02 \\ 0.02 \end{pmatrix} \text{ nm}^{-1}\end{split}\]

4. Derive the linear system

   To solve for \(\mathbf{D}\), let’s derive how the spot shifts relate to the displacement gradient. For any measured spot \(\mathbf{g}^{\text{meas}}\):

   \[\mathbf{g}^{\text{meas}} = (\mathbf{I} - \mathbf{D}^T)\mathbf{g}^{\text{ref}}\]

   Writing this out in components for a single spot:

   \[\begin{split}\begin{pmatrix} g_x^{\text{meas}} \\ g_y^{\text{meas}} \end{pmatrix} = \begin{pmatrix} 1-D_{xx} & -D_{yx} \\ -D_{xy} & 1-D_{yy} \end{pmatrix} \begin{pmatrix} g_x^{\text{ref}} \\ g_y^{\text{ref}} \end{pmatrix}\end{split}\]

   Multiply this out:

   \[\begin{split}g_x^{\text{meas}} &= (1-D_{xx})g_x^{\text{ref}} - D_{yx}g_y^{\text{ref}} \\ g_y^{\text{meas}} &= -D_{xy}g_x^{\text{ref}} + (1-D_{yy})g_y^{\text{ref}}\end{split}\]

   Rearranging to get spot shifts \(\Delta g = g^{\text{meas}} - g^{\text{ref}}\):

   \[\begin{split}\Delta g_x &= -D_{xx}g_x^{\text{ref}} - D_{yx}g_y^{\text{ref}} \\ \Delta g_y &= -D_{xy}g_x^{\text{ref}} - D_{yy}g_y^{\text{ref}}\end{split}\]

   For two spots (\(\mathbf{g}_1\) and \(\mathbf{g}_2\)), this gives us four equations:

   \[\begin{split} \begin{pmatrix} \Delta g_{1x} \\ \Delta g_{1y} \\ \Delta g_{2x} \\ \Delta g_{2y} \end{pmatrix} = \begin{pmatrix} -g_{1x}^{\text{ref}} & 0 & -g_{1y}^{\text{ref}} & 0 \\ 0 & -g_{1x}^{\text{ref}} & 0 & -g_{1y}^{\text{ref}} \\ -g_{2x}^{\text{ref}} & 0 & -g_{2y}^{\text{ref}} & 0 \\ 0 & -g_{2x}^{\text{ref}} & 0 & -g_{2y}^{\text{ref}} \end{pmatrix} \begin{pmatrix} D_{xx} \\ D_{xy} \\ D_{yx} \\ D_{yy} \end{pmatrix}\end{split}\]

5. Solve for displacement gradient

Invert the system to find the displacement gradient tensor \(\mathbf{D}\):

\[\begin{split}\mathbf{D} = \begin{pmatrix} D_{xx} & D_{xy} \\ D_{yx} & D_{yy} \end{pmatrix} = \begin{pmatrix} 0.01 & -0.01 \\ -0.01 & -0.01 \end{pmatrix}\end{split}\]

6. Calculate strain tensor

The strain tensor \(\boldsymbol{\varepsilon}\) is the symmetric part of \(\mathbf{D}\):

\[\begin{split}\boldsymbol{\varepsilon} = \frac{1}{2}(\mathbf{D} + \mathbf{D}^T) = \begin{pmatrix} 0.01 & -0.01 \\ -0.01 & -0.01 \end{pmatrix}\end{split}\]

This gives us:

• Normal strain \(\varepsilon_{xx} = 0.01\) (1% tensile strain in x)

• Normal strain \(\varepsilon_{yy} = -0.01\) (1% compressive strain in y)

• Shear strain \(\varepsilon_{xy} = \varepsilon_{yx} = -0.01\) (1% shear)