Fourier
Fourier transform basics
- What does the Fourier transform do?
The Fourier transform converts a function defined in the time or spatial domain into a frequency-domain representation. The transform shows which frequencies are present, and the complex result encodes amplitude and phase for each frequency.
- How is the continuous Fourier transform defined?
- \[F(u) = \int_{-\infty}^{\infty} f(x)\, e^{-i2\pi u x}\, dx\]
The transform is complex. The amplitude and phase are given by
\[A(u) = \sqrt{\Re\{F(u)\}^2 + \Im\{F(u)\}^2} \qquad \phi(u) = \tan^{-1}\!\left(\frac{\Im\{F(u)\}}{\Re\{F(u)\}}\right)\]
Common Fourier transform properties
- Why does multiplication by \(i\) in Fourier space correspond to differentiation in real space?
The derivative property states:
\[\mathcal{F}\left\{\frac{df}{dx}\right\} = i 2\pi u \cdot F(u)\]where \(F(u)\) is the Fourier transform of \(f(x)\). In discrete form with wavenumber \(k\):
\[\mathcal{F}\left\{\frac{df}{dx}\right\} = ik \cdot F(k)\]Intuition: Taking a derivative measures how fast a function changes. High-frequency components (large \(k\)) change rapidly, so they contribute more to the derivative. Multiplying by \(ik\) in Fourier space automatically weights each frequency by its rate of oscillation, giving the derivative in real space after inverse transform.
Why the \(i\) factor? The \(i\) arises from the derivative of \(e^{ikx}\):
\[\frac{d}{dx}e^{ikx} = ik \cdot e^{ikx}\]Since Fourier transforms decompose functions into \(e^{ikx}\) components, differentiating brings down a factor of \(ik\) for each component.
- How does the shift theorem work?
Shifting a function in real space adds a linear phase ramp in Fourier space:
\[\mathcal{F}\{f(x - x_0)\} = e^{-ikx_0} F(k)\]Intuition: A shift doesn’t change which frequencies are present, only their relative phases. The phase ramp \(e^{-ikx_0}\) encodes the shift distance \(x_0\). This is why SSB uses phase ramps to track probe positions.
Reverse direction: Similarly, multiplying by a phase ramp in real space shifts in Fourier space:
\[\mathcal{F}\{e^{ik_0 x} f(x)\} = F(k - k_0)\]- What are some common Fourier transform pairs?
These pairs build intuition for how features in real space map to Fourier space:
Gaussian transforms to Gaussian:
\[f(x) = e^{-\pi x^2} \quad \Leftrightarrow \quad F(k) = e^{-\pi k^2}\]Gaussians are special—they remain Gaussian after Fourier transform (self-similar).
Box function transforms to sinc:
\[\begin{split}f(x) = \begin{cases} 1 & |x| \leq a \\ 0 & |x| > a \end{cases} \quad \Leftrightarrow \quad F(k) = \frac{\sin(2\pi ka)}{\pi k}\end{split}\]Sharp edges (box function) create oscillating patterns (sinc) in Fourier space. This is why rectangular apertures create diffraction rings.
Delta function transforms to constant:
\[f(x) = \delta(x - x_0) \quad \Leftrightarrow \quad F(k) = e^{-ikx_0}\]A point in real space contains all frequencies equally (pure phase ramp in Fourier space).
Constant transforms to delta:
\[f(x) = 1 \quad \Leftrightarrow \quad F(k) = \delta(k)\]A constant (zero frequency) appears as a spike at \(k = 0\) in Fourier space.
- How do derivatives appear in 2D Fourier transforms?
For 2D functions \(f(x,y)\), partial derivatives become:
\[\mathcal{F}\left\{\frac{\partial f}{\partial x}\right\} = ik_x F(k_x, k_y)\]\[\mathcal{F}\left\{\frac{\partial f}{\partial y}\right\} = ik_y F(k_x, k_y)\]The gradient \(\nabla f = (\partial f/\partial x, \partial f/\partial y)\) becomes \((ik_x F, ik_y F)\) in Fourier space. This is exactly why SSB extracts the phase gradient—the \(i\phi(x,y)\) term becomes \((ik_x, ik_y)\) multiplied by \(\tilde{\phi}\).
Discrete Fourier transform (DFT)
- When do you use the discrete Fourier transform?
When your data are sampled you use the discrete Fourier transform. For a length \(N\) sequence \(x_n\):
\[X_k = \sum_{n=0}^{N-1} x_n\, e^{-i2\pi \frac{k n}{N}}, \qquad k = 0,\dots,N-1\]- What should I know about DFT properties?
For real-valued signals the DFT is conjugate-symmetric; usually you inspect \(k=0\) up to \(k=\lfloor N/2\rfloor\).
The DFT yields complex coefficients whose magnitudes give amplitudes and whose angles give phases.
2D Fourier transform
- How does the Fourier transform generalize to 2D?
A 2D continuous transform for \(f(x,y)\) is
\[F(u,v) = \iint_{-\infty}^{\infty} f(x,y)\,e^{-i\,2\pi\,(u x + v y)}\,dx\,dy\]- What is the discrete 2D DFT formula?
The discrete 2D DFT for an \(M\times N\) array is
\[F[u,v] = \sum_{x=0}^{M-1}\sum_{y=0}^{N-1} f[x,y]\;e^{-i\,2\pi\left(\frac{u x}{M}+\frac{v y}{N}\right)}\]
(Source code, png, hires.png, pdf)

2D sinusoidal grating (left) and its Fourier magnitude (right). The script lives in docs/source/notebooks/plot_fourier.py.
Image shift detection using Fourier methods
- What is the problem we are solving?
Suppose you have two images that show nearly the same scene but one is shifted relative to the other. You need to measure that translation accurately. Comparing the images pixel by pixel across all possible shifts is slow: for an image with N pixels you must check roughly N possible displacements, making the direct approach O(N²).
- What is real-space cross-correlation?
Cross-correlation measures similarity between two signals at different relative shifts. For two real images \(f\) and \(g\), the cross-correlation is defined as
\[(f \star g)(\tau) = \int f(x)\, g(x+\tau)\, dx.\]When \(g\) is simply \(f\) shifted by \(x_0\), the cross-correlation produces a peak at \(\tau = x_0\). You could compute this in real space by sliding one image over the other and computing the overlap integral at every offset, but that is computationally expensive.
- Why compute shift detection in Fourier space?
The Fourier shift theorem states that if \(g(x) = f(x - x_0)\) then
\[G(k) = e^{-i\,2\pi\, k\, x_0}\, F(k).\]The translation becomes a phase difference in frequency space. The Fourier convolution and correlation theorem lets you compute cross-correlation with just three FFTs:
\[f \star g = \mathcal{F}^{-1}\{ \overline{F(k)}\; G(k) \},\]where the overline denotes complex conjugation. This reduces the cost from O(N²) to O(N log N), making shift detection practical even for large images.
Phase correlation method
- What is phase correlation?
In practice the magnitude of the Fourier coefficients can vary with contrast and noise. Phase correlation normalises the cross-power spectrum to keep only phase differences (which encode translations). Define the cross-power spectrum
\[R(k) = \frac{\overline{F(k)}\,G(k)}{|\overline{F(k)}\,G(k)|}.\]Its inverse Fourier transform is ideally a sharp impulse at the translation \(x_0\). Phase correlation is robust to uniform brightness changes and some multiplicative contrast changes.
- When should I use phase correlation?
TBA
Spectral leakage and windowing
- What is spectral leakage?
Real-world images are finite and thus implicitly multiply the underlying continuous signal by a rectangular window (the image support). That abrupt truncation introduces discontinuities at the edges which cause spectral leakage: energy that would be concentrated at a few frequencies is spread into many others.
- What does “leaking power” mean?
“Leaking power” (spectral leakage) means that sharp transitions in the spatial domain create broad-band contributions in the frequency domain: instead of a small number of discrete peaks you get sidelobes and a smeared spectrum. Windowing reduces those sidelobes.
- How does windowing reduce spectral leakage?
Applying a smooth taper such as a 2D Hann (cosine) window reduces the discontinuity at the border and significantly reduces leakage. The Hann window gently grades the image intensity to zero at the edges, trading a small loss in spatial extent for much cleaner Fourier magnitudes.
Below is a small demo comparing the FFT magnitude before and after applying a 2D Hann window.
(
Source code,png,hires.png,pdf)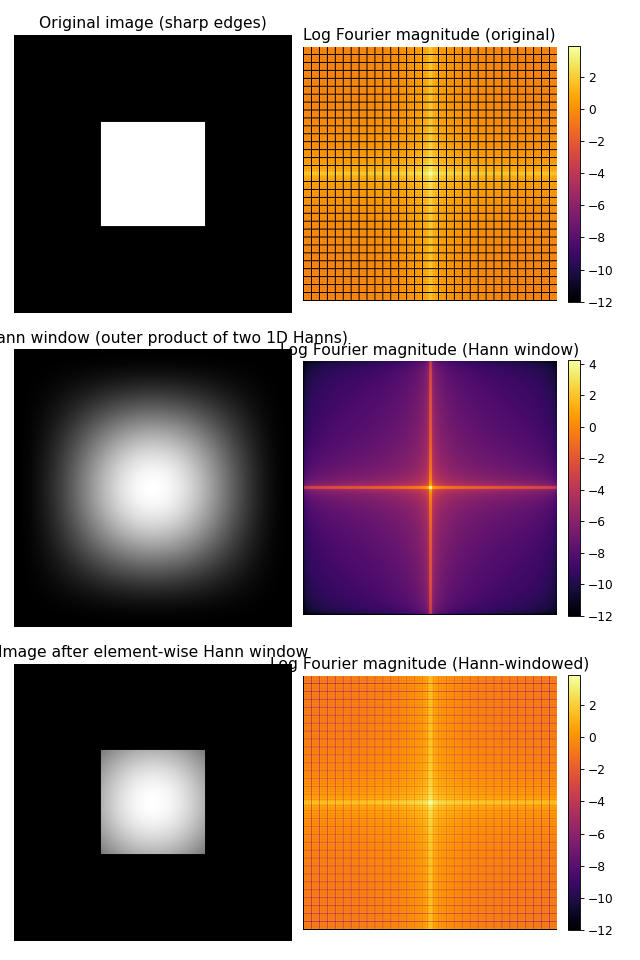
Left column: original square patch (top) and Hann-windowed image (bottom). Right column: their log Fourier magnitudes. The script is at
docs/source/notebooks/plot_hann_window_clean.py.
Advanced topics
- Why use Fourier space for solving the Poisson equation?
TBA
- What is the intuition behind 2D images and their Fourier transforms with k values?
TBA
- Why is Fourier space more effective for filtering and blurring?
TBA
- What do phase and amplitude represent in Fourier space?
TBA
- What is DC and low-frequency removal?
TBA